20회 ADP 실기 python 통계분석(데이터 처리)
in ADP on Adp
데이터 처리 Part
해당 부분은 데이터마이닝에서도 포함이 될 수는 있지만
일단은 통계분석으로 넣은 이유는 데이터 마이닝에서 해당 분석법이 안 쓰일 수 있고
일단 ADP 쪽 데이터마이닝에서의 핵심은 모델링이기 때문이다
그렇기에, 데이터마이닝에서도 포함이 되긴 하지만,
통계분석에서도 해당 분석법을 사용하여서 분류분석 단계로 넘어갈 수 있을 정도의 분석법들을 정리하고자 한다.
총 항목은 5개로
결측치 시각화 및 피벗테이블 등 통계분석시 나올 만한 가공법
값 scaling
PCA, FA
군집분석 Kmeans
반응변수 샘플링(under, over, smote)
로 진행해보려 한다.
import os
import numpy as np
import pandas as pd
pd.set_option('display.max_row', 500)
pd.set_option('display.max_columns', 30)
from pandas import DataFrame
import warnings
warnings.filterwarnings("ignore")
결측치 시각화 및 처리, 피벗테이블 등 데이터 가공
간단한 EDA로 데이터의 결측치를 시각화 하고 제거하거나 대체하는 방법을 간단하게 해놓고
이러한 류의 데이터가 아닌 피벗테이블 같은 방식으로 그룹화를 해서 진행을 해야될 경우를 위하여
피벗테이블로 가공을 하는 방법도 해놓았다.
데이터는 타이타닉 데이터를 사용하였고, 다운을 받으려면 https://www.kaggle.com/c/titanic/data 에서 받기 바랍니다.
train = pd.read_csv("train.csv")
print(train.shape)
train.head()
(891, 12)
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
missingno 패지키를 사용하면 전체 데이터에서 결측치가 있는 부분은 흰색 선이 나오고
값이 있는 데이터는 정상적인 검정색으로 나온다
import missingno
missingno.matrix(train)
<AxesSubplot:>

전체 데이터에서의 null의 총 갯수를 보고 싶으면 isnull을 쓰고 sum을 하면 된다
train.isnull().sum()
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64
Age 같은 경우는 그나마 결측치 비율이 작으므로 평균 값으로 대체를 하고 진행을 해보았다
train.loc[train.isnull()['Age'],'Age'] = train['Age'].mean()
train.isnull().sum()
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 0
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64
Cabin은 결측치가 많으므로 해당 열을 삭제하고 Embarked의 경우 2개만 결측치이므로 dropna로 해당 열만 삭제하였다
train2 = train.drop(columns=['Cabin']).dropna(axis=0)
train2.isnull().sum()
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 0
SibSp 0
Parch 0
Ticket 0
Fare 0
Embarked 0
dtype: int64
그 다음으로는 피벗테이블화 시켜서 그룹별로 원하는 값을 뽑아내는 방법입니다.
피벗테이블로 성별, 생존별 나이의 중앙값을 구한 방법입니다.
margins를 사용하는 경우, 전체에 대한 것도 같이 구해줍니다.
pivot1 = pd.pivot_table(train2, index='Sex', columns='Survived', values='Age', aggfunc='mean', margins=True)
pivot1
| Survived | 0 | 1 | All |
|---|---|---|---|
| Sex | |||
| female | 26.023272 | 28.797265 | 28.077094 |
| male | 31.175224 | 27.631705 | 30.505824 |
| All | 30.415100 | 28.423600 | 29.653446 |
만든 피벗 테이블에 unstack이나 stack을 해주면 해당 인덱스와 컬럼이 series 형식으로 풀리며
이 상황에서 reset_index를 해주면 피벗테이블을 만들면서 넣은 열들의 그룹별로의 값이 담긴 DataFrame이 만들어진다
pivot1.unstack().reset_index()
| Survived | Sex | 0 | |
|---|---|---|---|
| 0 | 0 | female | 26.023272 |
| 1 | 0 | male | 31.175224 |
| 2 | 0 | All | 30.415100 |
| 3 | 1 | female | 28.797265 |
| 4 | 1 | male | 27.631705 |
| 5 | 1 | All | 28.423600 |
| 6 | All | female | 28.077094 |
| 7 | All | male | 30.505824 |
| 8 | All | All | 29.653446 |
pivot1.stack().reset_index()
| Sex | Survived | 0 | |
|---|---|---|---|
| 0 | female | 0 | 26.023272 |
| 1 | female | 1 | 28.797265 |
| 2 | female | All | 28.077094 |
| 3 | male | 0 | 31.175224 |
| 4 | male | 1 | 27.631705 |
| 5 | male | All | 30.505824 |
| 6 | All | 0 | 30.415100 |
| 7 | All | 1 | 28.423600 |
| 8 | All | All | 29.653446 |
피벗 테이블을 단순하게 만드는 것이 아닌, 여러 열을 더 넣고 하려면 list 안에 넣고 하면 된다
pd.pivot_table(train2, index=['Sex','Parch'], columns='Survived', values='Age', aggfunc='median')
| Survived | 0 | 1 | |
|---|---|---|---|
| Sex | Parch | ||
| female | 0 | 28.000000 | 29.699118 |
| 1 | 28.500000 | 28.349559 | |
| 2 | 16.000000 | 22.000000 | |
| 3 | 48.000000 | 24.000000 | |
| 4 | 37.000000 | NaN | |
| 5 | 39.000000 | 38.000000 | |
| 6 | 43.000000 | NaN | |
| male | 0 | 29.699118 | 29.699118 |
| 1 | 28.000000 | 6.000000 | |
| 2 | 26.000000 | 3.500000 | |
| 3 | 16.000000 | NaN | |
| 4 | 52.000000 | NaN | |
| 5 | 39.000000 | NaN |
pd.pivot_table(train2, index=['Sex','Parch'], columns=['Survived','SibSp'], values=['Age','Fare'], aggfunc='median')
| Age | Fare | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Survived | 0 | 1 | 0 | 1 | |||||||||||||||||||||
| SibSp | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 0 | 1 | 2 | 3 | 4 | |
| Sex | Parch | ||||||||||||||||||||||||
| female | 0 | 29.699118 | 27.000000 | 18.0 | NaN | NaN | NaN | NaN | 29.699118 | 29.699118 | 41.349559 | 31.5 | NaN | 8.05000 | 14.4583 | 18.0000 | NaN | NaN | NaN | NaN | 13.00000 | 52.55000 | 37.3646 | 18.425 | NaN |
| 1 | 18.000000 | 28.500000 | NaN | 29.699118 | NaN | NaN | NaN | 25.000000 | 34.500000 | 4.000000 | NaN | NaN | 14.45420 | 15.3729 | NaN | 25.46670 | NaN | NaN | NaN | 33.00000 | 29.50000 | 19.2583 | NaN | NaN | |
| 2 | 29.699118 | 25.000000 | 15.0 | 5.500000 | 7.5 | 16.0 | 29.699118 | 23.000000 | 23.000000 | 19.500000 | 23.5 | 11.0 | 17.72915 | 151.5500 | 34.3750 | 27.90000 | 31.27500 | 46.9 | 69.55 | 24.17915 | 53.28960 | 262.3750 | 263.000 | 19.65625 | |
| 3 | NaN | 48.000000 | NaN | NaN | NaN | NaN | NaN | 24.000000 | 54.000000 | 24.000000 | NaN | NaN | NaN | 34.3750 | NaN | NaN | NaN | NaN | NaN | 19.25830 | 23.00000 | 18.7500 | NaN | NaN | |
| 4 | 29.000000 | 45.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 21.07500 | 27.9000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 5 | 40.000000 | 39.000000 | NaN | NaN | NaN | NaN | NaN | NaN | 38.000000 | NaN | NaN | NaN | 34.40625 | 31.2750 | NaN | NaN | NaN | NaN | NaN | NaN | 31.38750 | NaN | NaN | NaN | |
| 6 | NaN | 43.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 46.9000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| male | 0 | 29.699118 | 29.699118 | 28.0 | NaN | NaN | NaN | NaN | 29.699118 | 31.500000 | 39.849559 | NaN | NaN | 8.05000 | 21.0000 | 21.6792 | NaN | NaN | NaN | NaN | 13.43125 | 54.27085 | 78.4500 | NaN | NaN |
| 1 | 40.000000 | 33.000000 | 23.0 | 15.849559 | 7.0 | NaN | NaN | 14.500000 | 6.000000 | 1.000000 | NaN | NaN | 61.67920 | 24.1500 | 11.5000 | 23.27085 | 39.68750 | NaN | NaN | 37.91665 | 17.32500 | 39.0000 | NaN | NaN | |
| 2 | 38.500000 | 27.849559 | NaN | 10.000000 | 6.5 | 10.0 | 29.699118 | 4.000000 | 6.000000 | NaN | NaN | 3.0 | 69.63750 | 25.6000 | NaN | 27.90000 | 31.33125 | 46.9 | 69.55 | 37.00420 | 120.00000 | NaN | NaN | 31.38750 | |
| 3 | NaN | 16.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 34.3750 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 4 | NaN | 52.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 145.4500 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 5 | NaN | 39.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 31.2750 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
값 scaling
값 scaling 같은 경우는 각 변수들마다 평균과 분산의 크기가 다른 경우가 많을텐데
표준화 단계를 통해서 데이터의 왜곡으로 인한 문제를 피할 수 있게 해줍니다.
train, test로 나누어서 scaling을 할 때에는 train의 값을 이용해서
test data에 적용을 해줘야지, train은 train끼리 test는 test끼리 적용을 하면 안됩니다.
f_train = pd.read_csv("https://rfriend.tistory.com/attachment/cfile21.uf@2577A64555C56ECF0CF0C8.csv",
encoding='cp949')
del f_train['company']
f_train.head()
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| 0 | 2.43 | 11.10 | 18.46 | 441.67 | 0.90 |
| 1 | 3.09 | 9.95 | 29.46 | 239.43 | 0.90 |
| 2 | 2.22 | 6.86 | 28.62 | 249.36 | 0.69 |
| 3 | 5.76 | 23.19 | 23.47 | 326.09 | 1.43 |
| 4 | 1.60 | 5.64 | 25.64 | 289.98 | 1.42 |
MinMaxScaler는 최소값과 최대값을 각각 0과 1이 되게 해주는 스케일링이며
StandardScaler는 평균과 표준편차를 이용해서 하는 방법이다.
test data에 적용하고 싶은 경우는 Scaler에 transform(test_data)를 하면 된다
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaled = standardScaler.fit_transform(f_train)
scaled_data = DataFrame(standardScaled, columns=f_train.columns)
scaled_data.head()
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| 0 | -0.548158 | 0.393974 | -0.944859 | 1.377781 | 0.052140 |
| 1 | 0.049833 | 0.134995 | -0.320690 | -0.077102 | 0.052140 |
| 2 | -0.738427 | -0.560872 | -0.368354 | -0.005667 | -0.545097 |
| 3 | 2.468975 | 3.116637 | -0.660579 | 0.546316 | 1.559452 |
| 4 | -1.300176 | -0.835615 | -0.537447 | 0.286547 | 1.531012 |
scaled_data.describe().iloc[0:3]
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| count | 1.800000e+01 | 1.800000e+01 | 1.800000e+01 | 18.000000 | 1.800000e+01 |
| mean | 2.097088e-16 | 8.635068e-17 | -2.898916e-16 | 0.000000 | 1.788693e-16 |
| std | 1.028992e+00 | 1.028992e+00 | 1.028992e+00 | 1.028992 | 1.028992e+00 |
표본 갯수가 애초에 작아서 std가 값이 1보다는 살짝은 큰 모습입니다.
하지만 어느정도 평균은 0에 가까운 모습을 보이고 있기에
원하는 대로 scaling이 완료된 모습입니다.
from sklearn.preprocessing import MinMaxScaler
min_max_scaler = MinMaxScaler()
MinMax_train = min_max_scaler.fit_transform(f_train)
MinMax_train = DataFrame(MinMax_train, columns=f_train.columns)
MinMax_train.head()
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| 0 | 0.199519 | 0.381269 | 0.018769 | 0.927889 | 0.595420 |
| 1 | 0.358173 | 0.322416 | 0.225225 | 0.459112 | 0.595420 |
| 2 | 0.149038 | 0.164278 | 0.209459 | 0.482129 | 0.435115 |
| 3 | 1.000000 | 1.000000 | 0.112800 | 0.659983 | 1.000000 |
| 4 | 0.000000 | 0.101842 | 0.153529 | 0.576283 | 0.992366 |
MinMax_train.describe().T[['min','max']]
| min | max | |
|---|---|---|
| V1 | 0.0 | 1.0 |
| V2 | 0.0 | 1.0 |
| V3 | 0.0 | 1.0 |
| V4 | 0.0 | 1.0 |
| V5 | 0.0 | 1.0 |
최소값과 최대값이 확실히 0과 1인 것을 확인할 수 있습니다.
둘 중 제시되는 방법을 사용하시거나
둘을 비교하는 문제가 나올 경우에는 둘 다 수행한 뒤에
생각하시는 장단점을 서술하는 방식으로 하시면 될 듯 합니다.
PCA & FA
이 둘의 차이점에 대한 포스팅은
https://ysyblog.tistory.com/124 해당 블로그를 보시면 자세히 보실 수 있습니다
PCA는 데이터 마이닝쪽에서 나올 가능성이 높고,
만약에 나온다면 PCA에 사용된 변수들은 버리고 pca로 나온 변수들을 사용해서 하면 됩니다.
FA가 나온다면 통계분석 영역에서 나올 가능성이 높습니다.
굳이 pca가 있는데 fa를 머신러닝에서 사용하는 경우는 본 적이 없습니다.
PCA
표준화 된 데이터로 학습을 시키고 pca componenents의 구성요소대로 변환을 수행한 다음에 score에 저장합니다.
pca.components_로 변수들이 어떻게 묶였는지 볼 수는 있지만
높은 값을 가지고 있는 변수들 끼리 묶어서 어떠한 변수로 이름을 지어보겠다는 가능하지
높은 값을 가진 것들만 사용하는 것은 안됩니다.
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(scaled_data )
score = pca.transform(scaled_data)
pca.components_
array([[ 0.07608427, -0.39463007, 0.56970191, -0.5598277 , -0.44778451],
[ 0.77966993, 0.56541218, 0.16228156, -0.19654293, 0.08636803],
[ 0.0008916 , -0.29532165, 0.24122211, -0.25659729, 0.88811827],
[ 0.1407554 , -0.11764417, 0.63772189, 0.74809431, 0.00366842],
[-0.60540325, 0.65078503, 0.42921686, -0.14992183, 0.05711464]])
ratio는 각 주성분들이 전체 데이터에서 가지고 있는 분산 비율입니다.
제2주성분까지 합쳐보면 약 87퍼입니다.
ratio = pca.explained_variance_ratio_
ratio
array([0.55229245, 0.32113064, 0.11011261, 0.01281263, 0.00365167])
import matplotlib.pyplot as plt
ax = plt.plot(['PC1','PC2','PC3','PC4','PC5'], ratio)
plt.show()
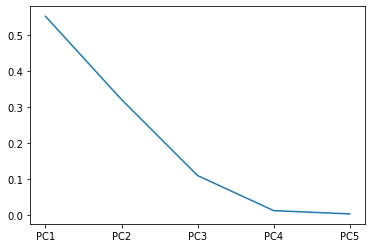
주성분에서 몇 개의 주성분까지만 선택할 고르는 방법은 기울기가 완만해지는 시점이나
전체 분산 비율이 70퍼에서 90퍼 정도 사이에 있으면 분석가의 판단하에 선택합니다.
3개를 선택해도 되긴 하지만 일단 2개만 선택하도록 하겠습니다.
pca = PCA(n_components=2)
pca_data = pca.fit_transform(scaled_data )
DataFrame(pca_data, columns=['PC1','PC2']).head()
| PC1 | PC2 | |
|---|---|---|
| 0 | -1.530135 | -0.624247 |
| 1 | -0.212363 | 0.082795 |
| 2 | 0.202561 | -0.998596 |
| 3 | -2.422543 | 3.607282 |
| 4 | -0.921329 | -1.497481 |
FA
같은 데이터로 FA도 해보고 싶지만, 원하는 방식대로 결과가 나오지 않아서
다른 데이터를 가지고 와서 수행하였습니다.
from factor_analyzer import FactorAnalyzer
df = pd.read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/psych/bfi.csv",
index_col=0)
df.drop(['gender','education','age'],axis=1,inplace=True)
df.dropna(inplace=True)
df.head(2)
| A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | C5 | E1 | E2 | E3 | E4 | E5 | N1 | N2 | N3 | N4 | N5 | O1 | O2 | O3 | O4 | O5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 61617 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | 4.0 | 3.0 | 3.0 | 3.0 | 4.0 | 4.0 | 3.0 | 4.0 | 2.0 | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 |
| 61618 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 4.0 | 1.0 | 1.0 | 6.0 | 4.0 | 3.0 | 3.0 | 3.0 | 3.0 | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 |
요인성 평가
- Bartlett test
귀무가설 : 탐색적 요인 분석에 적합한 데이터가 아니다.
- kmo 검정 (변수 최소 3개)
관측된 모든 변수간 분산 비율 추정
0.6미만은 부적절, 0.8이상은 우수
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
calculate_bartlett_sphericity(df)
(18170.966350869257, 0.0)
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all, kmo_model = calculate_kmo(df)
kmo_model
0.848539722194922
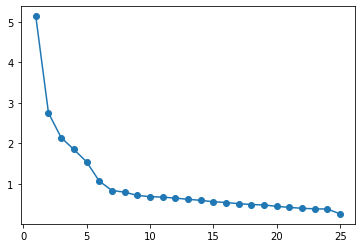
요인 수 선택
eigen value가 1이상일때 까지 혹은 기울기가 완만해지는 시점까지 진행
fa = FactorAnalyzer(n_factors = df.shape[1], rotation=None)
fa.fit(df)
ev, v = fa.get_eigenvalues()
ev
array([5.13431118, 2.75188667, 2.14270195, 1.85232761, 1.54816285,
1.07358247, 0.83953893, 0.79920618, 0.71898919, 0.68808879,
0.67637336, 0.65179984, 0.62325295, 0.59656284, 0.56309083,
0.54330533, 0.51451752, 0.49450315, 0.48263952, 0.448921 ,
0.42336611, 0.40067145, 0.38780448, 0.38185679, 0.26253902])
plt.scatter(range(1,df.shape[1]+1),ev)
plt.plot(range(1,df.shape[1]+1),ev)
[<matplotlib.lines.Line2D at 0x22582431730>]
import seaborn as sns
fa = FactorAnalyzer(n_factors = 6, rotation=None)
fa.fit(df)
efa_result = pd.DataFrame(fa.loadings_, index = df.columns)
plt.figure(figsize=(6,10))
sns.heatmap(efa_result, annot=True, cmap='Blues', fmt='.2f');
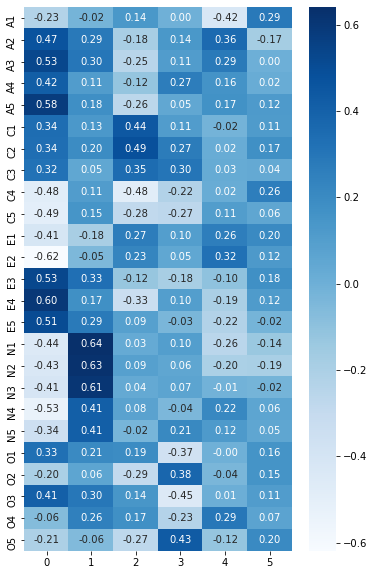
0부터 5까지 중에서
각각 0은 N, 1은 E, 2는 C, 3은 A, 4는 O에 대해서 높은 요인 적재량을 가진다
fa = FactorAnalyzer(n_factors = 5, rotation='varimax') #최대 우도 방법
fa.fit(df)
df1 = pd.DataFrame(fa.get_factor_variance())
df1.index = ['SS Loading','Proportion Var','Cumulative Var'] # ss loading = 각 factor의 설명력
df1
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| SS Loading | 2.709633 | 2.473090 | 2.041106 | 1.844498 | 1.522153 |
| Proportion Var | 0.108385 | 0.098924 | 0.081644 | 0.073780 | 0.060886 |
| Cumulative Var | 0.108385 | 0.207309 | 0.288953 | 0.362733 | 0.423619 |
cf) 신뢰도 계수 구하기
def CronbachAlpha(item):
item = np.asarray(item)
itemvars = item.var(axis=0, ddof=1)
tscores = item.sum(axis=1)
nitems = item.shape[1]
return (nitems/(nitems-1)) * (1 - (itemvars.sum() / tscores.var(ddof=1) ))
factors = ['A','C','E','N','O']
items_dict = {}
for factor in factors:
items_dict[factor] = [x for x in df.columns if x[0] == factor]
for key, value in items_dict.items():
print(key)
print(CronbachAlpha(df[value]))
print()
A
0.4437533019387808
C
-0.31628341382240494
E
-0.6552429584732491
N
0.8169468842774033
O
-0.176098107937655
마이너스가 아닌 N과 A가 신뢰도가 높다고 할 수 있는 듯 하다.
군집분석(Kmeans) (som은 패키지가 없고 직접 구현해야함)
군집분석에 대한 설명은 som을 편하게 할 수 있는 R에서 자세히 하려고 하는데
비지도학습이다보니까 반응 변수가 필요 없고, 숫자 데이터들을 몇 개의 그룹으로 묶을지 해놓으면
새로 들어오는 데이터는 어떠한 그룹으로 들어가는지도 예측을 해주는 방식이다
from sklearn.cluster import KMeans
import numpy as np
X = np.array([[1, 2,3], [1, 4,2], [1, 0,0],
[10, 2,5], [10, 4,7], [1, 0,3]])
X = DataFrame(X)
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
kmeans.labels_
array([2, 2, 0, 1, 1, 0])
kmeans.predict([[0, 0,3], [12, 3,7]])
array([0, 1])
kmeans.cluster_centers_
array([[ 1. , 0. , 1.5],
[10. , 3. , 6. ],
[ 1. , 3. , 2.5]])
반응 변수 샘플링(under, over, smote)
smote의 경우, 범주형 변수가 있다면, 미리 one-hot encoding등을 사용해서 변환을 해줘야지 반응변수 샘플링이 가능하다.
under sampling과 over sampling은 단순하게 늘리거나 줄이는 방식이라 상관 없다.
from collections import Counter
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv'
df = pd.read_csv(url, header=None)
data = df.values
X, y = data[:, :-1], data[:, -1]
X[0]
array([1.52101e+00, 1.36400e+01, 4.49000e+00, 1.10000e+00, 7.17800e+01,
6.00000e-02, 8.75000e+00, 0.00000e+00, 0.00000e+00])
from imblearn.under_sampling import RandomUnderSampler
X_resampled, y_resampled = RandomUnderSampler(random_state=0).fit_resample(X, y)
Counter(y_resampled)
Counter({1.0: 9, 2.0: 9, 3.0: 9, 5.0: 9, 6.0: 9, 7.0: 9})
from imblearn.over_sampling import RandomOverSampler
X_resampled, y_resampled = RandomOverSampler(random_state=0).fit_resample(X, y)
Counter(y_resampled)
Counter({1.0: 76, 2.0: 76, 3.0: 76, 5.0: 76, 6.0: 76, 7.0: 76})
from imblearn.over_sampling import SMOTE
X_resampled, y_resampled = SMOTE(random_state=0).fit_resample(X, y)
Counter(y_resampled)
Counter({1.0: 76, 2.0: 76, 3.0: 76, 5.0: 76, 6.0: 76, 7.0: 76})
20회 ADP 실기를 준비하면서 만든 notebook 파일에 대한 깃허브 링크 입니다.
